知识分享 | 浅谈ANOVA一般线性模型(GLM)的高效应用
2022-03-10
01
开篇语
上一篇文章,咱们交流了“双样本T测试分析方法应用的场景”(请查阅文末链接文章)。双样本T测试应用在自变量为1个X即单一因子的情况下,但通常在数据分析中,更多的是面临有多个自变量X即多因子Xs的情形,今天就给大家分享一种高效的、能同时分析多因子多水平的一般线性模型(GLM)的应用方法。
02
一般线性模型(GLM)的应用案例
分析影响客户满意度的温度和时间的配置问题:
1. 收集数据如下:
|
温度 |
时间 |
满意度评分结果 |
|
350 |
8 |
60 |
|
350 |
10 |
65 |
|
350 |
15 |
70 |
|
400 |
8 |
62 |
|
400 |
10 |
68 |
|
400 |
15 |
70 |
|
450 |
8 |
69 |
|
450 |
10 |
75 |
|
450 |
15 |
80 |
|
350 |
8 |
65 |
|
350 |
10 |
63 |
|
350 |
15 |
72 |
|
400 |
8 |
63 |
|
400 |
10 |
70 |
|
400 |
15 |
75 |
|
450 |
8 |
70 |
|
450 |
10 |
76 |
|
450 |
15 |
82 |
|
350 |
8 |
63 |
|
350 |
10 |
66 |
|
350 |
15 |
73 |
|
400 |
8 |
65 |
|
400 |
10 |
72 |
|
400 |
15 |
76 |
|
450 |
8 |
71 |
|
450 |
10 |
78 |
|
450 |
15 |
85 |
2. 运用GLM分析的重要步骤
Minitab软件操作路径:统计 → 方差分析 → 一般线性模型(GLM)
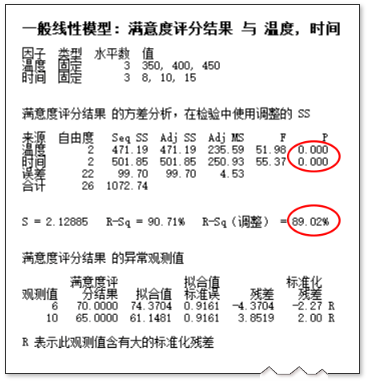
结论:”温度”和”时间”能够解释89.02%的满意度评分结果。
注意:须继续研究残差
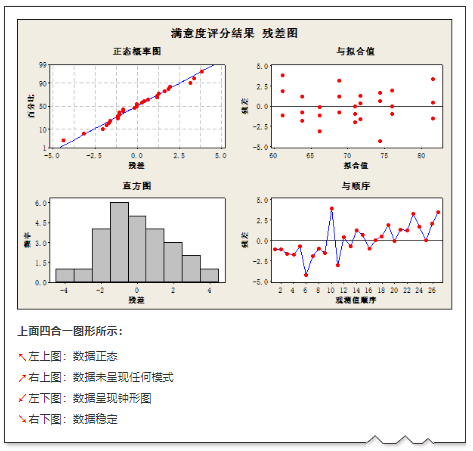
左上图和右下图的补充图示如下:
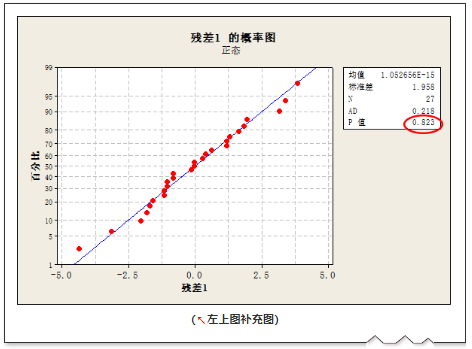
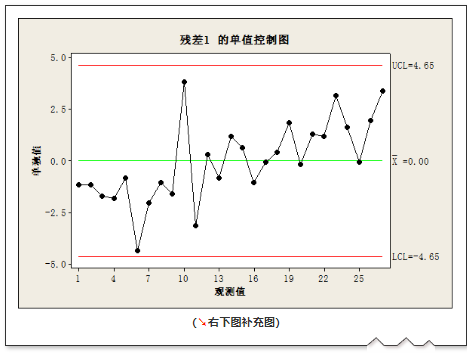
3. 研究各单一因子的显著性
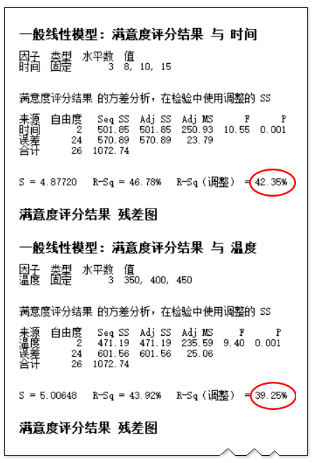
结论:“时间”能够解释42.35%,“温度”能够解释39.25%。
注意:继续研究残差(无异常,略)
4. 通过描述性统计评估最好的因子配置
Minitab软件操作路径:统计 → 表格 → 描述性统计
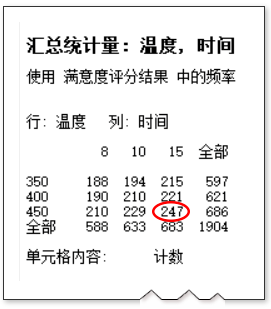
结论:在“时间”为“15”,“温度”为“450”的配置下,继续优化,提高顾客满意度的评分结果。
03
结束语
一般线性模型(GLM)是一种非常高效的数据分析的工具。若朋友们希望进一步了解或掌握一般线性模型(GLM)的操作细节,请与文思特咨询老师联系。
若朋友们对MSA、SPC、DOE、回归、双样本T测试分析感兴趣,请查阅以下链接的相关文章。
相关文章推荐如下
![]()
↓↓







